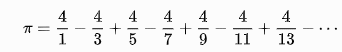
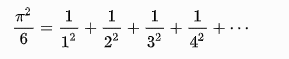
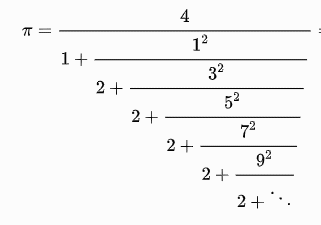
Looping with for and range()exercises

If we add up the numbers  1 + 1/2 + 1/3 + 1/4 + 1/5 + ... 1/n  we'll get some number larger than 1.

Ex. 1:  Create the function sumHarmonic(n) that adds up all of the reciprocals of the numbers from 1 to n.  Calculate sumHarmonic(100) and put it into the Comments-to-Teacher

Ex. 2: Calculate how  many terms of the series above (yes, it's called the "Harmonic Series") will it take to get a sum that is larger than 10?  You may want to modify sumHarmonic() to stop when the sum becomes larger than 10.  Put your answer into the Comments-to-Teacher.

OPTIONAL:

And now to pi...

First of all, since pi is an irrational number, a computer cannot hold its exact value, so let's agree that we'll call

pi = 3.141592653589793

Look at the table below.  Each series is labeled with the mathematician who discovered it.  There have now been very many series that have been discovered that can be used to calculate pi -- the first 3 below are just some of the more famous ones.

In each of the series, the more terms you use, the closer the calculation on the right gets to the value on the left.  For instance, for Leibniz, the sum on the right is sometimes bigger and sometimes smaller than pi, but gets closer and closer to it.

Create the functions Leibniz(teeny), Wallis(teeny), Euler(teeny), and  as a challenge, Lange(teeny).  Each of these functions will be given a very small number (like 0.001, or even 0.000001), and the function must calculate how many terms of the series on the right to use so that the sum or product or continued-fraction is within this small amount of the value on the left hand side.

As an example, for Wallis, how many pairs of numbers (like 4/3,4/5) must you multiply together to get within teeny of pi/2 (e.g. abs(pi/2 - product) < teeny)

As mentioned above, Lange(teeny) is a challenge problem and is more difficult than it looks because it has to be calculated from the bottom up.

Be careful in testing, do not choose very small values of teeny (like 0.00001) initially while you are not yet confident of the code.  Instead try 0.1 initially, while you are debugging.

For Leibniz(teeny), Euler(teeny) and Lange(teeny), can you find a simple relationship between the value of teeny and the what these functions return when given teeny?  If so, write it into the Comments-to-Teacher.
Mathematician Series
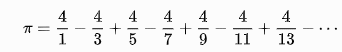Leibniz Leibniz pi
Wallis
Euler
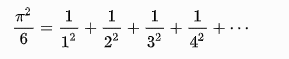L.J.Lange (1999)
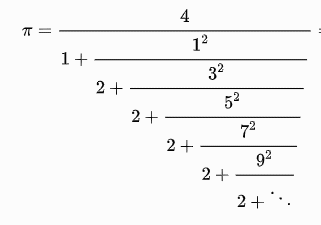