Python Exercises #3
Loops with for and range() and some while

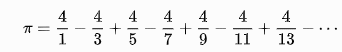
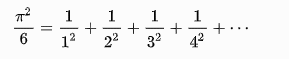
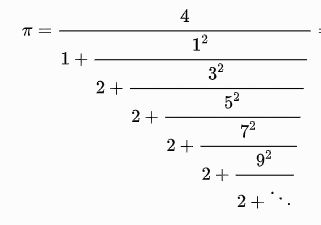
We are looking at the "Harmonic series", namely SumHarmonic(n) = 1 + 1/2 + 1/3 + 1/4 + ... 1/n

def SumHarmonic(n):
    total = 0
    for i in range(1,n+1):
        total += 1/i
    return total
    
def SumHarmonicTotal(total):
    so_far = 0
    for i in range(1,1000000):  # guess this number
        so_far += 1/i
        if so_far >= total:
            return i

def SumHarmonicTotalBetter(total):
    # In this version, we won't need to guess
    so_far = 0
    i = 0
    while so_far < total:
        i += 1
        so_far += 1/i
    return i

def SumHarmonicTotal_MuchWorse(total):
    # This version finds the answer, but very inefficiently (will take much longer when total > 9).  Can you guess why?
    n = 1
    trial = SumHarmonic(n)
    while trial < total:
        n += 1
        trial = SumHarmonic(n)
    return n

Leibniz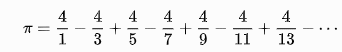
Wallis
Euler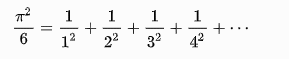
Lange (1999)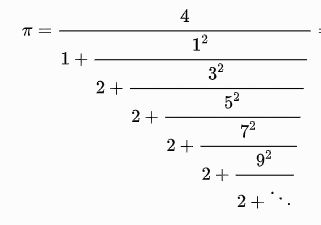

pi = 3.141592653589793 

def Leibniz(teeny):
    so_far = 0
    i = 1
    while abs(pi - so_far) > teeny:
        denom = 2 * i - 1
        if i % 2 == 1:
            so_far += 4/denom
        else:
            so_far -= 4/denom
        i += 1
    return i - 1

def Wallis(teeny):
    so_far = 1
    i = 1
    while abs(pi/2 - so_far) > teeny:
        numer = (2*i)**2
        denom = (2*i-1)*(2*i+1)
        so_far *= numer/denom
        i += 1
    return i - 1

def Euler(teeny):
    so_far = 0
    i = 1
    while abs(pi*pi/6 - so_far) > teeny:
        so_far += 1/(i*i)
        i += 1
    return i - 1

def LangeContFrac(n):
    # calculate the continued fraction to the depth n, from the bottom up
    frac = 1
    for i in range(n,0,-1):
        numer = (2*i-1)**2
        dfrac = numer / frac
        if i == 1:
            frac = 1 + dfrac 
        else:
            frac = 2 + dfrac
    return 4/frac
    
def Lange(teeny):
    i = 1
    while abs(pi - LangeContFrac(i)) > teeny:
        i += 1
    return i - 1

# print out results for various teeny sizes...
for i in range(1,4):
    teeny = 1/10**i
    print('teeny:',teeny,'Leibniz:',Leibniz(teeny),'Wallis:',Wallis(teeny),'Euler:',Euler(teeny),'Lange:',Lange(teeny))
    
    teeny: 0.1 Leibniz: 10 Wallis: 4 Euler: 10 Lange: 10
    teeny: 0.01 Leibniz: 100 Wallis: 39 Euler: 100 Lange: 100
    teeny: 0.001 Leibniz: 1000 Wallis: 393 Euler: 1000 Lange: 1000

Notice that for Leibniz, Euler and Lange, the number of terms necessary is 1/teeny. That's the interesting pattern that wants explanation...